LRUCache 的实现

Tech

文引

要实现 LRU Cache，我们需要了解 LRU Cache 的运行原理。

LRU Cache

LRU (Least Recently Used) Cache 是一种缓存淘汰算法，最少最近使用的Cache。也就是说，在淘汰的时候，淘汰的是最长时间未使用（或者使用最少）的数据

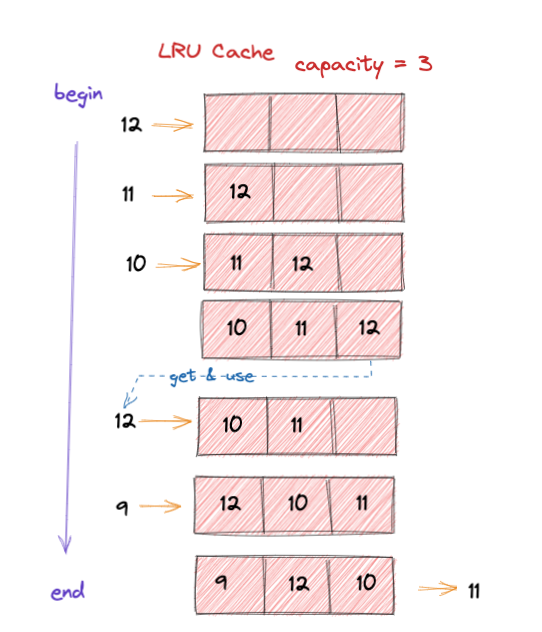
如下图，容量是为 3 的缓存:

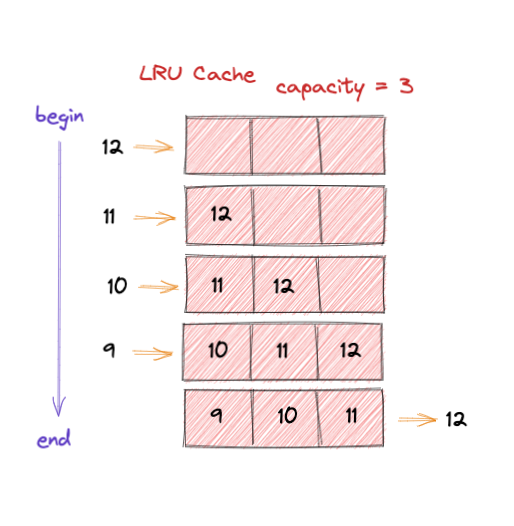
lru-cache-run

  • 一开始，Cache 为空,添加一个 12 元素进入，后面依次放入了 11 和 10。这时候将缓存填满了。
  • 将放入 9 的时候，因为缓存满了，需要移除最长时间未使用的数据。所以 12 被移除，9 被加入。

P.S.: 这边未考虑使用操作，其实也可以想像的到，如果要是使用了，就将使用的元素从缓存移除，重新加入到缓存中

lru-cache-run-use

经过上述了解，已经直到了 LRU 的运行机制，这样我们总结特点：

  • Cache 大小固定有限
  • Cache Full 后，后续操作都需要执行 LRU 操作
  • Cache 操作支持并发
  • Cache 的 添加、排序、获取 尽量都是 O(1) 操作

Structure of LRU Cache

要考虑设计 LRU Cache，我们需要根据其特点来设计：

  • 特性1: LRU Cache 是一个 Queue，如果 Queue 里面的某个元素被访问了，它应该被迁移到淘汰的末位。
  • 特性2:LRU Cache 要有固定容量（内存有限）, 当新加一个元素的时候，是添加到 Queue Head；当发送淘汰的时候，淘汰的是 Queue Tail。（FIFO）
  • 特性3: 查找命中缓存的数据，必须在 最少的固定的时间内 完成。也就是我们我们必须尽量保证时间复杂度 O(1)
  • 特性4: 移除最近最少使用的元素，也必须在 最少的固定的时间内 完成。同上 O(1)

要满足 特性1 和 特性2 还是很简单的,要实现一个 Queue 我们可以使用数据结构 固定大小的Linked List 或 固定大小的Array List 做实现。 但是在兼顾 特性3 的时候，可以想象到要尽量 添加、命中 都是 O(1) 操作，在 Queue 中基本不可能。但是我们可以预判到 HashMap 可以最大化的解决这个问题， 因为HashMap最理想的情况下达到 命中缓存为 O(1) 操作，到此，我们发现 LRU Cache 的设计应该是 HashMap + List； 下面再去考虑 特性4，在 Cache 满的情况下，考虑每次添加新的元素都要执行LRU策略，这时候可预见的对于这个 List的插入``删除比查询多， 肯定选择是 Linked List，且是 DoublyLinkedList 不是 SingleLinkedList (出于操作O(1)考虑)

至此, 可见 LRU Cache 的实现是 HashMap + DoublyLinkedList 的结合，如下图：

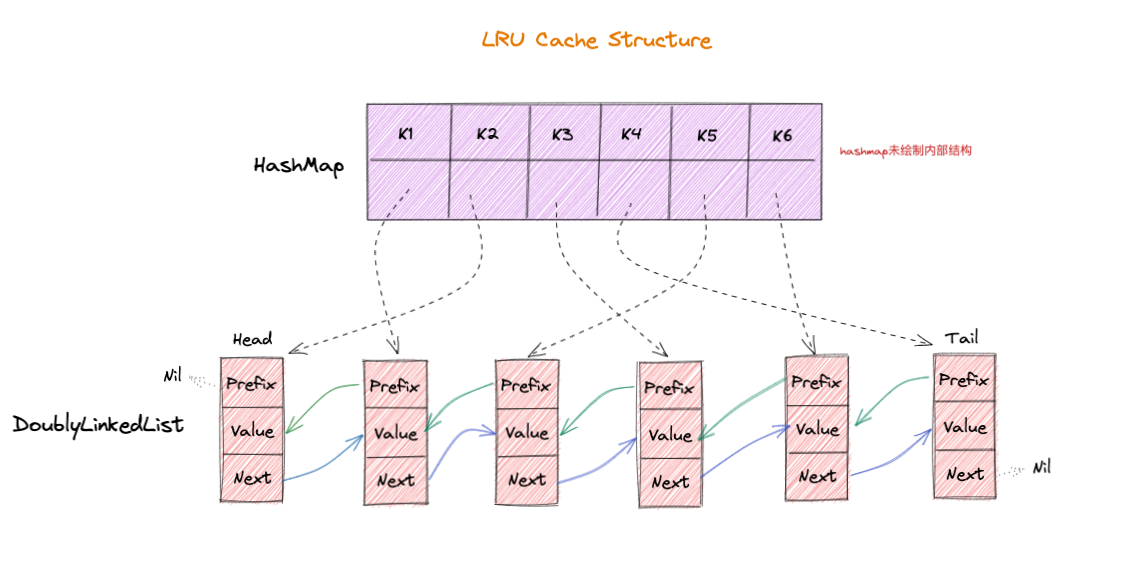
lru-cache-run

Key 存储到HashMap内部，Value 为 指向的 链表元素(Element(Key,Value))指针，这样在获取的时间可以快速访问到缓存数据

LRU缓存算法：

如果 Key 存在 HashMap中，则 缓存命中，否则，缓存未命中。

发生命中:

  • 移除 LinkedList 命中的元素，并把该元素重新加入到 LinkedList 头部
  • 更新 HashMap 中 Key 对应 LinkedList 头引用

未命中:

  • 在 LinkedList 头添加一个新元素
  • 在 HashMap 中添加新元素，并且引用刚刚加入的 LinkedList 的头元素

Implementation In Code

定义 Cache 接口

public interface Cache<K,V> {
    Optional<V> get(K k);
    boolean put(K k, V v);
    int size();
    //....
}

定义 Cache Element

public class CacheElement<K, V> {
    private K key;
    private V value;
    //...
}

实现 LRU Cache, 核心 get(k), put(k,v), evict()

核心实现

public class LruCache<K, V> implements Cache<K,V> {

    private int size;
    private Map<K, DoublyLinkedList.Node<CacheElement<K,V>>> nodeHashMap;
    private DoublyLinkedList<CacheElement<K,V>> doublyLinkedList;

    public LruCache(int size) {
        this.size = size;
        this.nodeHashMap = new HashMap<>(size);
        this.doublyLinkedList = new DoublyLinkedList<>();
    }
    //......
}

get(k)

    public Optional<V> get(K k) {
        DoublyLinkedList.Node<CacheElement<K, V>> e = nodeHashMap.get(k);
        if (e != null) {
            return Optional.of(e.getV().getValue());
        }
        return Optional.empty();
    }

put(k, v)

    public boolean put(K k, V v) {
        CacheElement<K, V> element = new CacheElement<>(k, v);
        //找寻到了 key
        DoublyLinkedList.Node<CacheElement<K,V>> node;
        if (nodeHashMap.containsKey(k)) {
            DoublyLinkedList.Node<CacheElement<K,V>> n = nodeHashMap.get(k);
            node = doublyLinkedList.updateAndMoveToFront(n, element);
        } else {
            // 判断队列的大小 和 配置的指定大小是否一致是否已满
            if (size() >= size) {
                //执行LRU策略
                evict();
            }
            node = doublyLinkedList.add(element);
        }
        nodeHashMap.put(k, node);
        return true;
    }

    private boolean evict() {
        DoublyLinkedList.Node<CacheElement<K, V>> node = doublyLinkedList.removeTail();
        nodeHashMap.remove(node.getV().getKey());
        return true;
    }

DoublyLinkedList

定义

public class DoublyLinkedList<T> {
    
    private int size;
    private Node<T> head;
    private Node<T> tail;
    
    public static class Node<T> {
        T v;
        Node<T> prefix;
        Node<T> next;
        public Node(T t, Node<T> prefix, Node<T> next) {
            this.v = t;
            this.prefix = prefix;
            this.next = next;
        }

        public T getV() {
            return v;
        }
    }
    public DoublyLinkedList() {
        clear();
    }
    //.......
}

removeTail()

    public Node<T> removeTail() {
        Node<T> old = tail;
        if (old == head) {
            clear();
        } else {
            tail = tail.prefix;
            tail.next = null;
            old.prefix = null;
            size--;
        }
        return old;
    }

add(t)

    public Node<T> add(T element) {
        // 添加到头节点添加每次
        Node<T> node = new Node<>(element, head, head);
        if (head == null) {
            head = tail = node;
            head.prefix = null;
            tail.next = null;
        } else {
            head.prefix = node;
            head = node;
            head.prefix = null;
            tail.next = null;
        }
        size++;
        return head;
    }

updateAndMoveToFront(n,e)

    public Node<T> updateAndMoveToFront(Node<T> n, T element) {
        removeTail();
        return add(element);
    }

上面代码实现在 github 代码

留坑

在多线程情况下需要考虑并发, 这边未考虑。

  • HashMap 考虑使用 ConcurrentHashMap
  • DoublyLinkedList 操作的时候添加 ReentrantReadWriteLock
  • LruCache 操作的时候添加 ReentrantReadWriteLock
comments powered by Disqus